10月23日(火)の5校時に、5年1組の教室で算数の校長参観授業を行いました。単元名は「分数をもっとくわしく調べよう」で、ねらいは「約分の意味について理解する。」です。












まず、担任の古屋先生が、本時の学習問題を提示しました。
「18/24と大きさの等しい分数は、㋐、㋑のどちらの仲間に入りますか。」
㋐ 2/3、4/6、6/9、8/12・・・・
㋑ 3/4、6/8、9/12、12/16・・・・
子ども達は静かに集中し、ノートに熱心に書き写していました。








子ども達のノートを写真に撮影しましたが、さすが5年生できれいに視写していることが分かりますね! 前時の学習でも、図を上手に使いながら自分の考えをまとめています!








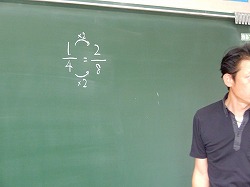









古屋先生の指導の素晴らしさは、充分時間をかけて「見通し」を全員にしっかり持たせ、全員が自分なりに自力で課題解決ができるようにしていることです。そのために、まず、「㋐と㋑がどういう分数のグループか分かる?」と問いかけ、既習事項を想起させ、分数の分母と分子に同じ数をかけても分数の大きさは変わらないことを確認しました。その上で、子ども達と話し合いながら、次の2つの「見通し」をクラス全体で共通理解しました。
<見通し1>18/24の分母と分子を同じ数でわる
<見通し2>分母が24になるところまで考える
「見通し」を時間をかけて丁寧に全員が共通理解できるようにしたことで、この後の展開を子ども達にとって主体的な学習とすることができます。





































写真を見ていただくと分かると思いますが、困った表情で鉛筆が止まって、停滞してしまっている子どもがほとんどいません。皆、自分なりの考えで学習問題を解決していっています。それでも、勘違いやケアレスミスをしてしまう子どもは当然いますので、古屋先生はきめ細かく机間巡視を行い、そうした子ども達に適切な指導をしています。
子ども達のノートの記述を写真に写しましたが、実に多様な方法であったり、表現方法であったりして課題を解決していることがおわかりになると思います。
・単純に分母と分子を2倍、3倍、4倍・・・として、18/24になるのを見つけている子。
・㋐は分母と分子をそれぞれ8倍すると分母が24になることを、そして、㋑を6倍すると分母が24になることをそれぞれ見つけて計算した子。
・マトリックス表を作って、分母が24になる分数を見つける子。
など、いろいろなやり方の子がいました。こうした多様性のある自力解決ができるのも、「見通し」に時間をかけて丁寧に行ったからだと思います。



















古屋先生が机間巡視を丁寧に行ったもうひとつの成果として、3名の子どもを意図的指名して、3つの代表的な解法を板書させました。
①の子は、文章と式を使って記述し、18/24の分母と分子を6で割ると3/4になり、答は㋑になることを示しました。
②の子は、分数を記述することで、2/3と3/4のそれぞれの分子と分母を2倍、3倍、4倍・・・していくと、3/4が18/24になることを示しました。
③の子は、分数の図示で、2/3の分母と分子を8倍すると16/24になり、3/4の分母と分子を6倍すると18/24になることを示しました。
この3つの解法が示されることにより、学級の子ども達は代表的な考え方を理解できるとともに、最も効率的な方法を考え出すことができます。
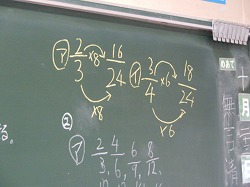









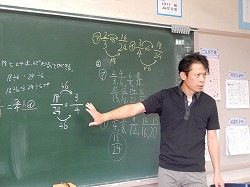






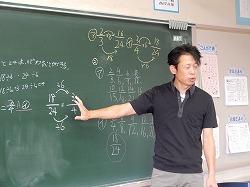




①~③の方法の中で最も効率的なやり方を全員で考え、その中から、③の子の記述方法を使いながら、①の子のやり方、つまり約分する方法が最も効率的であることを導き出しました。先生と子ども達で話し合っている最中の子どもの表情をたくさん掲載しましたが、お気づきだと思いますが、皆、集中して真剣に考え、自分なりの考えを生み出そうとしていることがよく分かりますね! この日は短縮授業で普段より5分間短かったので、最後のまとめをノートに記述することができず、それは次の算数の時間にすることになりましたが、古屋先生はチャイムが鳴ると子ども達の集中力が落ちてしまうことをよく理解していて、サッと授業を終了したことも感心しました。
見通しを大切にした、充実した主体的・対話的で深い学びの全員が理解でき、しかもレベルの高い授業をしていただいた古屋先生と、それに応えてとても高度な学びを実践した子ども達に大きな拍手を送ります!!
