11月16日(木)の2校時に5年1組の教室で算数の校長参観授業をしました。
単元名:面積の求め方を考えよう
本時のねらい:平行四辺形の面積の求め方を考え、説明することができる
です。





担任の金井先生は「今まで習ってきたことを使うと新しいことがわかるよ」と言って、学習コーナーを示しました。さりげなく、子ども達に「見通し」につながる既習事項を意識させています。





金井先生は、学習課題である「面積の求め方を考えよう」と板書し、次に「面積って何?」と聞くと、子ども達は「広さ!」と答えました。次に、先生は「面積は何を基にしているの?」と聞くと、子ども達は「1㎠が何個分かです」と答えました。「今までに習った面積の求め方は何ですか?」と聞くと、「正方形」と「長方形」と答え、さらに先生は面積の公式も確認し、それを黒板に貼った紙に書き込みました。ここまで何気ないやりとりのようですが、このことも今から示される問題の解決のための「見通し」であり、手がかりになっているのです。


次に、本時の問題「平行四辺形ABCDの面積の求め方を考えましょう。」を黒板に貼り、全員で確認しました。








さらなる見通しとして、子ども達の発言の中から「手がかりは正方形と長方形の面積」ということを確認し、次に、L字型の紙を示して「以前、これはどのようにして面積を求めましたか」と質問しました。子ども達は次の3つを答えました。
①つけたし作戦:欠けている部分にも紙があると仮定して面積を求め、欠けている部分の面積を引く方法
②バラバラ作戦:2つの長方形(含む正方形)に分けて面積を求める方法
③合体作戦:2つの長方形に分けてから、その2つをつなげて長い長方形を作ってから面積を求める方法
皆さんもお気づきのように、ここまでの学習の中で子ども達は十分に「見通し」を持つことができました。しかも、教師が一方的に確認するのではなく、子ども達の発言を基に学級全体で確認していました。














































先生は、子ども達に平行四辺形の描かれた方眼紙のプリントを全員に配りました。子ども達は、ノートに本時の問題を書き、平行四辺形の描かれたプリントを貼りました。こうすることにより、ノートが子ども達の課題解決のための道具になるとともに、学習の記録となります。先生は「図に説明を書き込んでもいいし、切ってもいい。式でも言葉でも書いていいですよ!」と助言しました。これにより子ども達は自分の考えを様々な方法で表現でき、それは表現の多様性を保障しているだけでなく、自力解決の後の全体での「つなぐ」学習で役立ちます!
いよいよ自力解決が始まりました! 先生は積極的に机間巡視をしながら、座席表にそれぞれの子ども達の考えを書き込みながら把握するとともに、手の動かない子には「黒板の〇〇作戦は使えるかなぁ?」と言いながら、ヒントを出したり、時には指導したりしていました。これがあるから「学び合い」の学習でも、全員の学習権が保障されるのです!
自力解決の後半の時間帯になると、特徴的な考え方の子に、大きなプリントを渡し、発表ができるよう準備させました! プリントをもらった子ども達は、嬉しそうに書き込んでいました!!





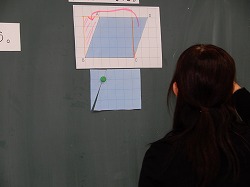
























いよいよ全体の学び合いが始まりました。つなぐ学習の流れは大きくは次の通りです。
①大きなプリントに書き込んだ子を指名して黒板にその方法を貼る
②貼ったプリントの方法を子ども達に解釈させ、プリントを作成した以外の子に考え方を説明させる(説明につなげる)
③プリントを作成した子以外の子にこれは何作戦か発表させる(既習の作戦につなげる)
④プリントを作成した以外の子に式を考えて発表させる(式につなげる)
こうして様々なものにつなげながら、プリントを作成した子の考えを全員で共有しました。私が感心したのは、この学習を通して解法の考えがつながるだけでなく、学級全員の心が一つにつながり、「全員で課題を解決している」という学級の強いつながりが湧き上がってくるのを感じました! 最終的に、全体の学び合いを通して3つの解法を全員で共有しました。子ども達は「まだあるよ!」とか「大きなプリントにやってみたい!」と言っていましたが、これが大切なのです!!













いよいよ本時の核心であるまとめに入りました。先生が「いろいろな方法で解決したのですが、共通していることはどんなこと?」と聞くと、子ども達は「長方形にしている」「3つの作戦を使っている」と答えました。今回、まとめとしてとても斬新な方法を活用したと思うのが、黒板に「まとめ」「平行四辺形の面積は( )求めることができる」と書き、( )の中の言葉を考えさせました。このようにすれば、子どもが自分の言葉で本時の学習をまとめることができます。(長方形にして考えれば)とまとまりました。
本時の最後に子ども達が書いた学習感想が素晴らしかったです。
「平行四辺形の面積の求め方が一つではなくたくさんあったので面白いと思いました。また、いくつかの方法も試したいです。」
「私は〇〇君の考え方が気がつかなかったのですごいなと思いました。」
「平行四辺形は長方形にして考えるとすごく簡単だなと思いました。考え方がたくさんあって面白かったです。」
学級全員を課題解決に向かわせ、全員の力で平行四辺形の面積の求め方を見つけさせることができた金井先生の的確な指導と、その指導に応え素晴らしい学習を展開した子ども達に大きな拍手を送ります!
